DCN网络结构

DCN模型以一个嵌入和堆叠层(embedding and stacking layer)开始，接着并列连一个cross network和一个deep network，接着通过一个combination layer将两个network的输出进行组合。

整体网络结构如下:

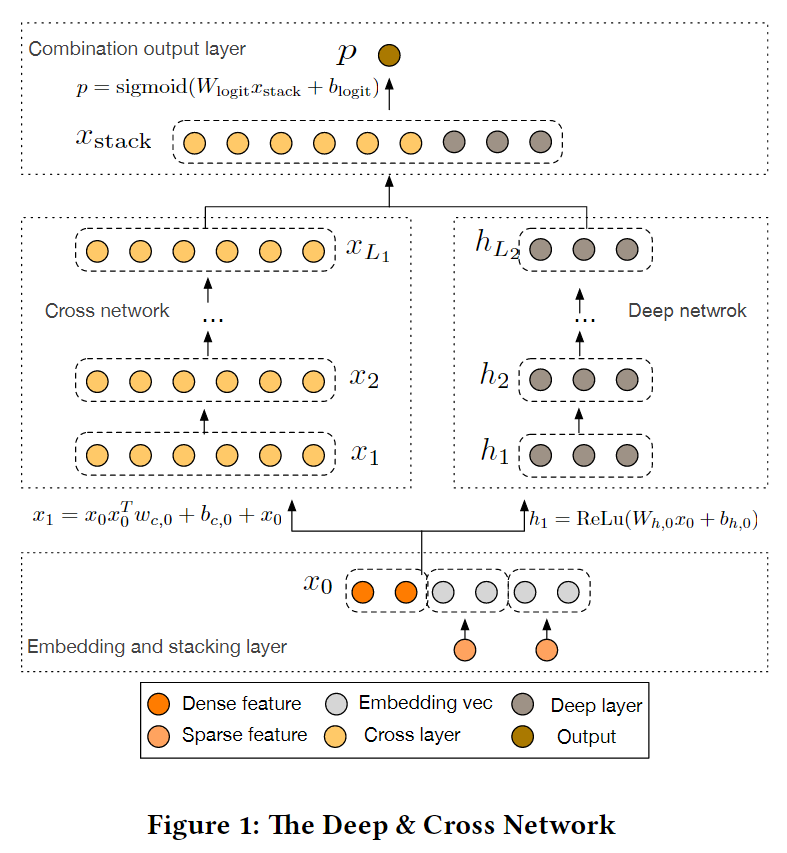
Embedding and Stacking Layer

在大规模推荐系统中，如CTR预测，通常会有大量的类别特征需要处理，如“country=usa”。为了将这些信息变成计算机能处理的特征，通常使用one_hot编码处理成独热向量如“[ 0,1,0 ]”；然而，这些大量的词汇往往导致处理后的特征空间维度过高。

为了减少维数，一种常用的做法是采用嵌入过程将这些离散特征转换成实数值的稠密向量（通常称为嵌入向量）：
$$
\mathbf { x } _ { \text { embed, } i } = W _ { \text { embed } , i } \mathbf { x } _ { i }
$$

其中 $x_{embed,i}$ 是embedding vector， $x_i$ 是第i个category的二元输入， $W_{embed,i} \in R^{n_e \times n_v}$ 是对应的embedding matrix，会与网络中的其它参数一起进行优化，$n_e$, $n_v$分别是embedding size和vocabulary size。

然后，我们将嵌入向量与连续特征向量叠加起来形成一个向量：
$$
x_0 = [ x_{embed,1}^T, …, X_{embed,k}^T, X_{dense}^T]。
$$

拼接起来的向量$X0$将作为我们Cross Network和Deep Network的输入.

这一部分在tensorflow中，使用tf.feature_columnAPI可以很容易实现，大致代码结构如下：

embed0 = tf.feature_column.embedding_column(...)
...
dense0 = tf.feature_column.indicator_column(...)
dense1 = tf.feature_column.numeric_column(...)
...
columns = [embed0, ..., dense0, dense1, ...]
x0 = tf.feature_column.input_layer(features, feature_columns)

Cross Network

在广告场景下，特征交叉的组合与点击率是有显著相关的，例如，“USA”与“Thanksgiving”、“China”与“Chinese New Year”这样的关联特征，对用户的点击有着正向的影响。换句话说，来自“China”的用户很可能会在“Chinese New Year”有大量的浏览、购买行为，而在“Thanksgiving”却不会有特别的消费行为。这种关联特征与label的正向相关性在实际问题中是普遍存在的，如“化妆品”类商品与“女性”，“球类运动配件”的商品与“男性”，“电影票”的商品与“电影”品类偏好等。因此，引入特征的组合是非常有意义的。而这部分正是FM存在的意义。

DCN的特点之一就在于提出了一个创新的结构来计算组合特征：

交叉网络的核心思想是以有效的方式应用显式特征交叉。交叉网络由交叉层组成，每个层具有以下公式：

$$
x_{l+1} = x_0 x_l^T w_l + b_l + x_l = f(x_l, w_l, b_l) + x_l
$$

其中:

$x_l,x_{l+1}$ 是列向量（column vectors），分别表示来自第l层和第(l+1)层cross layers的输出；
$w_l, b_l \in R^d$是第l层layer的weight和bias参数。

可以看到，交叉网络的特殊结构使交叉特征的程度随着层深度的增加而增大。多项式的最高程度（就输入X0而言）为L层交叉网络L + 1。如果用Lc表示交叉层数，d表示输入维度。然后，参数的数量参与跨网络参数为：d * Lc * 2 (w和b).

在完成一个特征交叉f后，每个cross layer会将它的输入加回去，对应的mapping function $f：R^d \rightarrow R^d$，刚好等于残差$x_{l+1} - x_l$，这里借鉴了残差网络的思想。这种方式有两个好处：

通过拟合残差的方式，提高权重的敏感度，更适合稀疏的输入。
方便网络整体的反向传播，提高网络训练效率。

ResNet的原理，参见笔记：http://leanote.com/s/5b0eaf5a7968705f10000002

Deep Network

深度网络就是一个全连接的前馈神经网络，每个深度层具有如下公式：

$$
h _ { l + 1 } = f \left( W _ { l } h _ { l } + b _ { l } \right)
$$

和传统DNN一样，input进来，简单的N层full-connected layer的叠加，所以参数量主要还是在deep侧。
参数数量为：$d∗m+m+(m2+m)∗(Ld−1)$
L_d denote the number of deep layers, m denote the deep layer size, d denote the input dimension.
Output

Combination Layer

将Cross layer和Deep layer两个并行网络出来的输出做一次concat，对于多分类问题，过一个softmax就OK了。

链接层将两个并行网络的输出连接起来，经过一层激活函数得到输出：

$$
p = \sigma \left( \left[ \mathbf { x } _ { L _ { 1 } } ^ { T } , \mathbf { h } _ { L _ { 2 } } ^ { T } \right] \mathbf { w } _ { \operatorname { logits } } \right)
$$

如果是二分类就是$sigmoid$激活函数，损失函数可用$logloss$，多分类就是$softmax$.

TensorFlow实现代码

https://github.com/RyanDeepLearning/Deep-Cross-Net

References:

赵大寳

推荐系统CTR实战——Deep & Cross